Cuando la mayoría de nosotros vemos una máquina de extracción de chiclosos arrancando en un paseo marítimo turístico, pensamos en dulce, dulce azúcar. Jean-Luc Thiffeault piensa en dulce, dulce matemática. Como matemático aplicado en la Universidad de Wisconsin-Madison, Thiffeault está particularmente interesado en la forma en que los materiales como el caramelo se mezclan: en la máquina, el dulce se estira y se dobla una y otra vez para incorporar aire y desarrollar su textura ligera y masticable. A medida que se tira, el rectángulo original de chicloso se estira cada vez más, su longitud crece exponencialmente en la misma proporción cada vez. Esa relación de estiramiento es lo que le interesa a Thiffeault.
contenido relacionado
- Chocolate a prueba de derretimiento, gomitas impresas en 3D y otras fascinantes patentes de dulces
Cuando una persona tira del caramelo, generalmente toma un trozo de caramelo y lo estira sobre un gancho, uniendo los dos extremos. Luego tomarán esa pieza doblada y la estirarán sobre el gancho nuevamente, doblando la longitud, y así sucesivamente. En otras palabras, "La forma humana de hacerlo es un factor de multiplicación de 2", dice Thiffeault. Los extractores mecánicos pueden funcionar mejor, a menudo produciendo números irracionales exóticos más grandes como sus factores de estiramiento.
Resulta que la extracción de caramelo puede ser modelada por un campo abstracto de matemáticas conocido como dinámica topológica, esencialmente el estudio de cambios a gran escala a largo plazo a lo largo del tiempo en un espacio matemático. (Si la palabra topológica suena familiar, apareció recientemente en las noticias como parte del Premio Nobel de Física de este año). La misma matemática que describe la extracción del caramelo también tiene aplicaciones más serias: muchos procesos industriales, incluidos el soplado de vidrio y la preparación de medicamentos, requieren los líquidos viscosos se mezclan de maneras que se parecen más a tirar el caramelo que a mezclar la crema con el café. "Si está tratando de remover cosas realmente viscosas, como las pastas de la industria farmacéutica, no puede simplemente sacudirlas", dice Thiffeault. "No es como mezclar pintura".
Thiffeault ha entendido la extracción de chiclosos como un ejemplo de mezcla viscosa durante mucho tiempo, pero solo recientemente ha investigado la historia de los extractores de chiclosos para descubrir sus secretos matemáticos. El resultado de esa excursión a las patentes históricas es su reciente artículo "Una historia matemática de extractores de chiclosos", publicado en el servidor de preimpresión arXiv en julio.
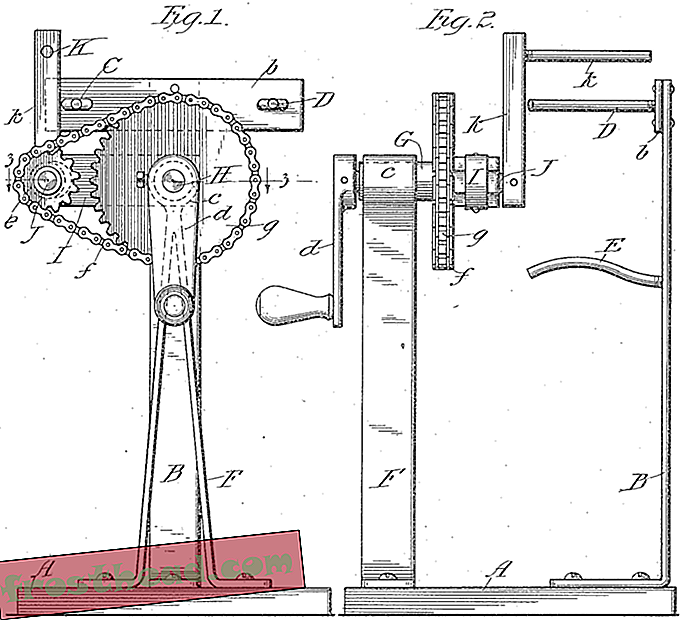Una imagen de una patente de máquina de chiclosas de 1916 que aparece en el estudio de Thiffeault. Específicamente, el área que condujo a su inmersión profunda en el extractor de chiclosos es el estudio de los llamados mapeos pseudo-Anosov. Pseudo-Anosov es una forma elegante de describir un proceso en el que una forma bidimensional se estira exponencialmente en una dirección mientras se contrae en la otra. Matemáticamente, el estudio de las asignaciones de pseudo-Anosov es relativamente nuevo. "En los años 70 y 80, la gente se esforzaba mucho por encontrar ejemplos", dice Thiffeault. Irónicamente, estuvieron allí todo el tiempo en patentes para extractores de chiclosos. "Debido a que los matemáticos nunca miraron esta literatura, nunca hubieran sabido que existían", dice.
Mientras estaba revisando las patentes de extractor de chiclosas, Thiffeault tropezó con una batalla legal que llegó hasta la Corte Suprema. La cuestión en el caso de 1921 Hildreth v. Mastoras fue cuán ampliamente debe interpretarse una patente de 1900 para un extractor de chicloso. Es decir: ¿fue un modelo posterior hecho por otra persona simplemente una mejora menor, o fue un dispositivo diferente? Una parte crucial del argumento fue cuán diferente era la patente de 1900 de un predecesor de 1893 (que probablemente nunca se fabricó). La opinión de la corte, escrita por el presidente del tribunal William Howard Taft, "muestra un profundo conocimiento de la dinámica topológica", escribe Thiffeault en su artículo.
El tribunal reconoció que el dispositivo anterior, que tenía solo dos ganchos, no podía haber estirado el caramelo hasta el grado exponencial requerido para la creación eficiente de dulces. La opinión de Taft dice:
Con solo dos ganchos, no podría haber lapeado de los dulces, porque no había un tercer pasador para volver a enganchar los dulces mientras se sostenía entre los otros dos pasadores. El movimiento de los dos pasadores en círculos concéntricos podría estirarlo un poco y agitarlo, pero no lo tiraría en el sentido de la técnica.
Thiffeault escribe: "La opinión de la Corte Suprema muestra la idea fundamental de que se requieren al menos tres barras para producir algún tipo de crecimiento rápido".
Thiffeault dice que hay dos extractores de chiclosos estándar en uso hoy en día, uno con tres barras y otro con cuatro. Sucede que tienen el mismo factor de estiramiento. Está relacionado con la llamada proporción de plata, 1+ √2, o alrededor de 2.414, un primo un poco menos luminoso de la más famosa proporción de oro.
El hecho de que los dos extractores de caramelo estándar se estiren con la proporción de plata es interesante porque la proporción de plata es, en un sentido matemático preciso, óptima. Sin embargo, Thiffeault advierte que no es tan fácil clasificar diferentes extractores de chiclosos, incluso cuando conoces sus factores de estiramiento: "Hay un aspecto de manzanas y naranjas que es bastante difícil de manejar", dice. Un extractor podría tener más barras y tardar más en volver a su estado inicial que otro, o podría requerir más torque o un engranaje más complicado. Entonces, aunque las matemáticas dan una idea de lo bien que tiran los extractores de chiclosas, no cuenta la historia completa.
La investigación de Thiffeault sobre los extractores de chiclosos lo inspiró a él y a su estudiante de pregrado Alex Flanagan a construir su propio modelo. Querían ver si podían aumentar la eficiencia sin modificar mucho los engranajes, y terminaron haciendo un nuevo extractor de 6 varillas basado en el engranaje del extractor estándar de 4 varillas. "La razón por la que pudimos hacerlo es que ahora tenemos matemáticas", dice Thiffeault. Podrían modelar ampliamente la máquina en la computadora y evitar una gran cantidad de pruebas y errores con dispositivos físicos reales que los inventores anteriores tuvieron que hacer. El dispositivo de 6 barras, que todavía es solo un prototipo, estira el caramelo aproximadamente el doble que los extractores estándar en cada ciclo.
Hasta ahora, los fabricantes de extractores de chiclosos no han estado golpeando exactamente la puerta de Thiffeault para obtener su consejo sobre la optimización de sus diseños (Big Taffy aparentemente está contento con su statu quo elástico), pero espera que sus métodos puedan tener efectos en otras industrias. Además del vidrio soplado, un lugar lógico para la optimización de mezclas es la industria farmacéutica. Después de todo, mezclar vitaminas y medicamentos requiere un control de calidad extremadamente alto: los fabricantes están "dispuestos a pagar mucho dinero por una mezcla perfecta" porque "no pueden tolerar un multivitamínico malo de 1000", dice Thiffeault. Entonces, algún día, los farmacéuticos pueden estar dando un dulce saludo a los devotos extractores de chiclosos de antaño.
Por otra parte, eso podría ser un poco exagerado.
