El 14 de marzo no es el Día del Pi este año. Los entusiastas de las matemáticas de todo el mundo celebran el evento como Ultimate Pi Day, porque la fecha corresponderá a los primeros cinco dígitos de pi (3.1415) en lugar de solo los primeros tres. Esta confluencia matemática no volverá a aparecer en un siglo, el 14 de marzo de 2115.
contenido relacionado
- El mundo está lleno de círculos.
Definido como la razón de la circunferencia de un círculo a su diámetro, pi ( π ) es un número trascendental e irracional, lo que significa que nunca se puede escribir como la razón de dos números enteros, y continúa indefinidamente sin ningún patrón repetitivo. Pi no es el único número irracional, también está el número de Euler (e) y la proporción áurea ( φ o phi), por ejemplo. Pero sigue siendo una fuente de fascinación porque sus orígenes son fácilmente explicables, dice Mario Livio, astrofísico del Space Telescope Science Institute en Maryland.
“Todos pueden entender cómo se deriva pi. Todos los otros números son más complejos. El número phi, por ejemplo, implica una división particular de una línea, y el número e requiere que sepas qué es un logaritmo ”, dice Livio, autor del libro Is God a Mathematician?
Otra gran parte del atractivo de pi es que tiene una extraña habilidad para aparecer en fórmulas matemáticas, muchas de las cuales son importantes para los procesos cotidianos, desde el procesamiento de imágenes hasta la navegación GPS. Aquí hay una pequeña muestra de las fórmulas de uso común que incluyen pi:
La transformada de Fourier
Llamada así por el matemático francés Jean-Baptiste Joseph Fourier, esta herramienta matemática descompone una señal en sus frecuencias componentes, más bien como un acorde musical puede descomponerse en sus notas componentes. En esencia, las transformadas de Fourier son ideales para procesar señales basadas en ondas como el sonido o la luz y para encontrar patrones. Eso hace que Fourier transforme una herramienta fundamental en el mundo digital moderno.
"Se le ha llamado el algoritmo más importante jamás desarrollado por la humanidad. Ahora eso puede ser una hipérbole, pero tal vez no lo sea ", dice Glen Whitney, fundador y director del Museo Nacional de Matemáticas en la ciudad de Nueva York. Las transformadas de Fourier se usan todo el tiempo para limpiar imágenes digitales, para autoajustar estrellas pop y para encontrar planetas lejanos que orbitan otras estrellas. La herramienta también es crucial para las funciones de voz a texto que ahora son estándar en los teléfonos inteligentes. "Cuando usas Siri o Google Now, uno de los primeros pasos es tomar tu voz y hacer una transformación de Fourier en ella ... resulta mucho más fácil reconocer las vocales cuando miras sus transformadas de Fourier que cuando miras señales originales en sí mismas ", dice Whitney.
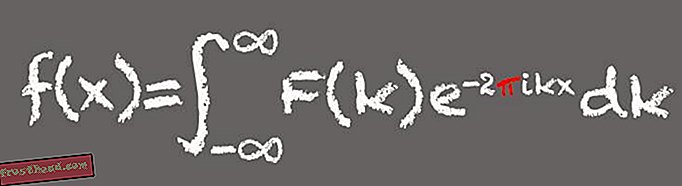(Ilustración de Victoria Jaggard) Pi aparece en la transformación de Fourier porque una de las partes componentes, o expresiones, de la fórmula está asociada con seno y coseno y los ángulos creados por una partícula que viaja alrededor de un círculo. "Siempre que tenga una fórmula que trate con círculos o ángulos, no se sorprenderá cuando aparezca pi", dice Whitney.
Principio de incertidumbre de Heisenberg
Uno de los pilares de la mecánica cuántica, el principio de incertidumbre de Heisenberg establece que un observador no puede conocer simultáneamente la posición y la velocidad de una partícula subatómica. En cambio, cuanto más precisamente se conoce la posición de una partícula, menos se puede saber sobre su velocidad.
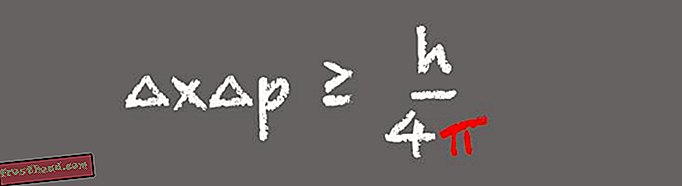(Ilustración de Victoria Jaggard) La aparición de pi en el principio de incertidumbre de Heisenberg tiene sentido cuando te das cuenta de que en la fórmula, la posición y el impulso son transformaciones de Fourier entre sí, dice Whitney. El principio de incertidumbre es importante en el mundo moderno porque describe el comportamiento de las partículas de luz, o fotones, en los sistemas de comunicaciones de fibra óptica. “Lo que nos dice es que no podemos conocer tanto la posición como el impulso de los fotones con extrema precisión. No se pueden diseñar protocolos de comunicación que violen el principio de incertidumbre de Heisenberg, porque no funcionarán ".
Ley de Stoke
La ley de Stoke calcula la fuerza necesaria para mover una esfera pequeña, es decir, un círculo tridimensional, a través de un fluido viscoso a cierta velocidad. Tiene aplicaciones en campos que van desde las ciencias de la Tierra hasta la medicina.
(Ilustración de Victoria Jaggard) "La ley se refiere específicamente al efecto de la viscosidad en una esfera en el fluido", dice Whitney, que es cómo entra en juego pi. En cuanto a los usos prácticos de la ley de Stoke, no busque más que su automóvil. "Durante décadas, la forma en que las compañías se aseguraron de que su aceite de motor tuviera la viscosidad adecuada para su automóvil fue, literalmente, colocar una serie de esferas de prueba en el aceite y medir el tiempo que les toma caer en el líquido", dice Whitney. Hoy en día, la forma más común de medir la viscosidad del aceite implica una herramienta llamada viscosímetro de tubo capilar, no se necesitan esferas, pero aún informa el resultado en unidades de medida llamadas centistokes.
Fórmula de Euler
El nombre del matemático suizo Leonard Euler, la versión de esta fórmula que incluye pi reúne algunos de los números más interesantes en matemáticas en un solo lugar:
(Ilustración de Victoria Jaggard) “Todos piensan que esto es increíble. Todos estos números que consideramos especiales aparecen en una hermosa ecuación ”, dice Livio. Si bien esta fórmula concisa puede inspirar asombro en los matemáticos, la forma más útil de la ecuación es un poco más larga:
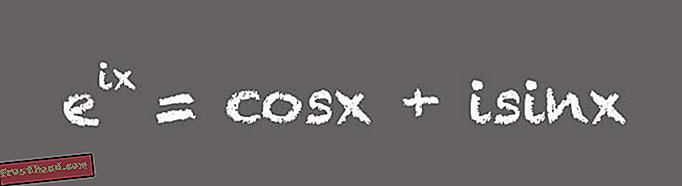(Ilustración de Victoria Jaggard) Esta versión desempaquetada de la fórmula de Euler es una herramienta increíble, dice Whitney. Por ejemplo, es importante para diseñar dispositivos electrónicos que utilizan corriente alterna o CA. "La fórmula de Euler en forma expandida significa que puede usar números complejos o imaginarios para analizar y diseñar circuitos de CA", dice Whitney. Esto se debe a que en un circuito de corriente alterna, el voltaje es una cantidad que oscila con el tiempo, generalmente 60 veces por segundo, por ejemplo, en el suministro eléctrico estándar de EE. UU. "La versión completa de la fórmula de Euler enseña cómo podemos usar números complejos como una forma abreviada conveniente para modelar fenómenos oscilantes", dice Whitney.
Ecuaciones de campo de Einstein
Un componente central de su teoría general de la relatividad, las ecuaciones de campo de Albert Einstein describen cómo la gravedad de la masa y la energía crean la curvatura del espacio-tiempo.
(Ilustración de Victoria Jaggard) "Describir que la curvatura involucra geometría, y dado que la definición original de pi proviene de la geometría, su apariencia en esta ecuación no es tan sorprendente", dice Livio. Además de revelar una verdad fundamental sobre cómo funciona el universo, la relatividad general tiene muchas aplicaciones prácticas. Por ejemplo, los satélites que componen el Sistema de Posicionamiento Global utilizado para la navegación estarían irremediablemente sincronizados entre sí si los ingenieros no tuvieran en cuenta los efectos de dilatación del tiempo pronosticados por la teoría.
